Automaton

  在介绍Automation类之前先介绍下有穷自动机的概念，有穷自动机分为确定型有穷自动机(DFA)跟不确定型有穷自动机(NFA)。由于本篇文章是为介绍TermRangeQuery作准备的，所以只介绍确定性有穷自动机。

确定型有穷自动机(Deterministic Finite Automaton)

  这种自动机在读任何输入序列后只能处在一个状态中，术语“确定型”是指这样的事实：在每个输入上存在且仅存在一个状态，自动机可以从当前状态转移到这个状态。

确定型有穷自动机的定义

  一个确定型有穷自动机包括：

• 一个有穷的状态集合，通常记作$Q$$Q$。

• 一个有穷的输入符号集合，通常记作 $\sum$$\sum$。

• 一个转移函数，以一个状态和一个输入符号作为变量，返回一个状态。转移函数通常记作$\delta$$\delta$。在表示自动机的图中，用状态之间的箭弧和箭弧上的标记来表示$\delta$$\delta$。如果$q$$q$是一个状态，$a$$a$是一个输入符号，则$\delta$$\delta$($q$$q$, $a$$a$)是这样的状态$p$$p$，使得从$p$$p$到$q$$q$有带$a$$a$标记的箭弧。

• 一个初始状态，是$Q$$Q$中状态之一。

• 一个终结状态或接受状态的集合$F$$F$。集合$F$$F$是$Q$$Q$的子集。

  通常用缩写DFA来指示确定型有穷自动机。最紧凑的DFA表示是列出上面5个部分，DFA可以用西面的五元组表示：

​ A = (Q，$\sum$$\sum$，$\delta$$\delta$，$q_0$$q_0$，$F$$F$)

  其中A是DFA的名称，$Q$$Q$是状态集合，$\sum$$\sum$是输入符号，$\delta$$\delta$是转移函数，$q_0$$q_0$是初始状态，$F$$F$是接受状态集合。

DFA如何处理串

  关于DFA需要理解的第一件事情是，DFA如何决定是否“接受”输入符号序列。DFA的"语言"是这个DFA接受的所有的串的集合。假设$a_1$$a_1$$a_2$$a_2$...$a_n$$a_n$是输入序列。让这个DFA从初始状态$q_0$$q_0$开始运行。查询转移函数$\delta$$\delta$，比如说$\delta$$\delta$($q_0$$q_0$，$a_1$$a_1$) = $q_1$$q_1$，以找出DFA A在处理第一个输入符号$a_1$$a_1$之后进入的状态。处理下一个输入符号$a_2$$a_2$，求$\delta$$\delta$($q_1$$q_1$，$a_2$$a_2$) 的值，假设这个状态是$q_2$$q_2$，以这种方式继续下去，找出状态$q_3$$q_3$，$q_4$$q_4$，...，$q_n$$q_n$，使得对每个$i$$i$, $\delta$$\delta$($q_{i-1}$$q_{i-1}$，$a_i$$a_i$) = $q_i$$q_i$。如果$q_n$$q_n$属于$F$$F$，则接受输入$a_1$$a_1$$a_2$$a_2$...$a_n$$a_n$，否则就“拒绝”。

例子

  形式化地规定一个DFA，接受所有仅在串中某个地方有01序列的0和1组成的串，可以把这个语言L写成： {$w$$w$ | $w$$w$形如x01y, x和y是只包含0和1的两个串}   这个语言中的串的例子包括01、11010和100011。不属于这个语言的串的例子包括0、1000、111000。   对于接受这个语言L的自动机，我们知道些什么？首先，输入字母是$\sum$$\sum$ = {0，1}。有某个状态集合$Q$$Q$，其中一个状态(如$q_0$$q_0$)是初始转态。这个自动机需要记住这样的重要事实：至此看到了什么样的输入。为了判定01是不是这个输入的一个字串，A需要记住：

1. 是否已经看到了01？如果是，就接受后续输入的每个序列，即从现在起只处在接受状态中。

2. 是否还没有看到01，但上一个输入是0，所以如果现在看到1，就看到01.并且接受从此开始看到的所有东西？

3. 是否还没有看到01，但上一个输入要么不存在(刚开始运行)，要么上次看到1？在这种情况下，A直到先看到0然后立即看到1才接受。

  这三个条件每个都能用一个状态表示。条件(3)用初始状态$q_0$$q_0$来表示。的确，在刚开始时，需要看到一个0然后看到一个1，但是如果在状态$q_0$$q_0$下接着看到一个1，就并没有更接近于看到01，所以必须停留在状态$q_0$$q_0$中。即，$\delta$$\delta$($q_0$$q_0$，1) = $q_0$$q_0$。   但是，如果在状态 $q_0$$q_0$下接着看到0，就处在条件(2)中，也就是说，还没有看到01，但看到了0。因此，用 $q_2$$q_2$来表示条件(2)。在输入0上从 $q_0$$q_0$出发的转移是$\delta$$\delta$($q_0$$q_0$，0) = $q_2$$q_2$。   现在，来考虑从状态 $q_2$$q_2$出发的转移。如果看到0，就并没有取得任何进展，但也没有任何退步。还没有看到01，但0是上一个符号，所以还在等待1。状态 $q_2$$q_2$完美地描述了这种局面，所以希望$\delta$$\delta$($q_2$$q_2$，0) = $q_2$$q_2$。如果在状态$q_2$$q_2$看到1输入，现在就知道有一个0后面跟着1.就可以进入接受状态，把接受状态称为$q_1$$q_1$，$q_1$$q_1$对应上面的条件(1)。就是说，$\delta$$\delta$($q_2$$q_2$，1) = $q_1$$q_1$。   最后，必须设计状态$q_1$$q_1$的转移。在这个状态下，已经看到了01序列，所以无论发生上面事情，都还是处在这样的局面下：已经看到01。也就是说，$\delta$$\delta$($q_1$$q_1$，0)==$\delta$$\delta$($q_1$$q_1$，1)=$q_1$$q_1$。   因此，$Q$$Q$ = {$q_0$$q_0$，$q_1$$q_1$，$q_2$$q_2$}，已经说过，$q_0$$q_0$是初始状态，唯一的接受状态是$q_1$$q_1$，也就是说，$F$$F$ = {$q_1$$q_1$}。接受语言L(有01字串的串的语言)的自动机A的完整描述是 A = ({$q_0$$q_0$，$q_1$$q_1$，$q_2$$q_2$}， {0，1}， $\delta$$\delta$，$q_0$$q_0$，{$q_1$$q_1$}) 其中$\delta$$\delta$是上面描述的转移函数。

转移图

根据上面的例子，生成的转移图如下： 图1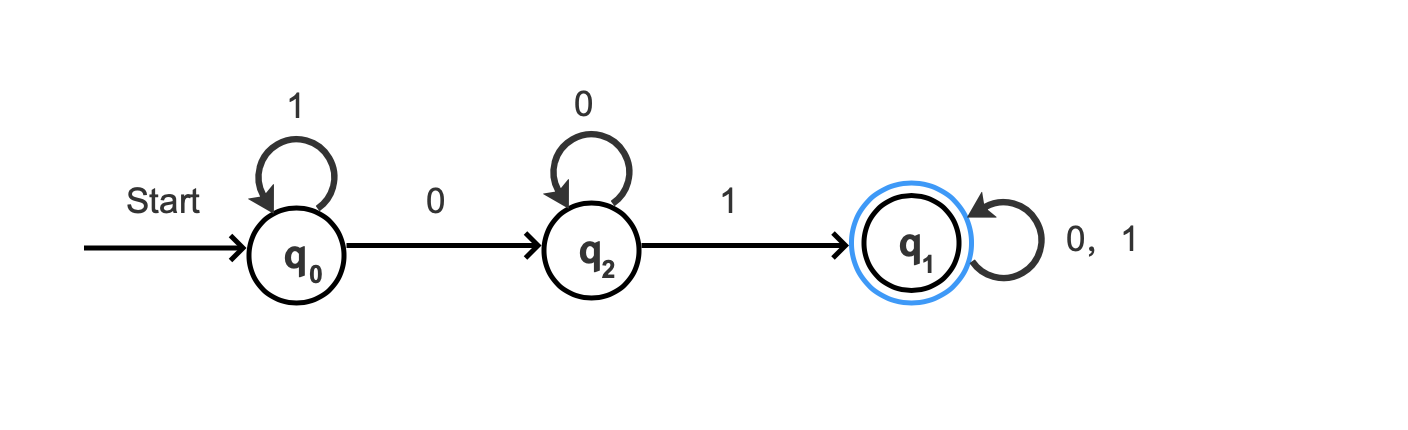： 蓝色圆圈表示当前状态只处在接受状态。

DFA在Lucene中的应用

  在Lucene，跟DFA相关功能有 通配符查询(WildcardQuery)、正则表达式(Regular Expression)、范围查询TermRangeQuery等。本篇文章中仅介绍TermRangeQuery。

TermRangeQuery中的DFA

  TermRangeQuery利用DFA来使得在查询阶段能获得查询范围的所有term，或者说所有的域值。我们直接通过一个例子来介绍DFA。

例子

  索引阶段的数据： 图2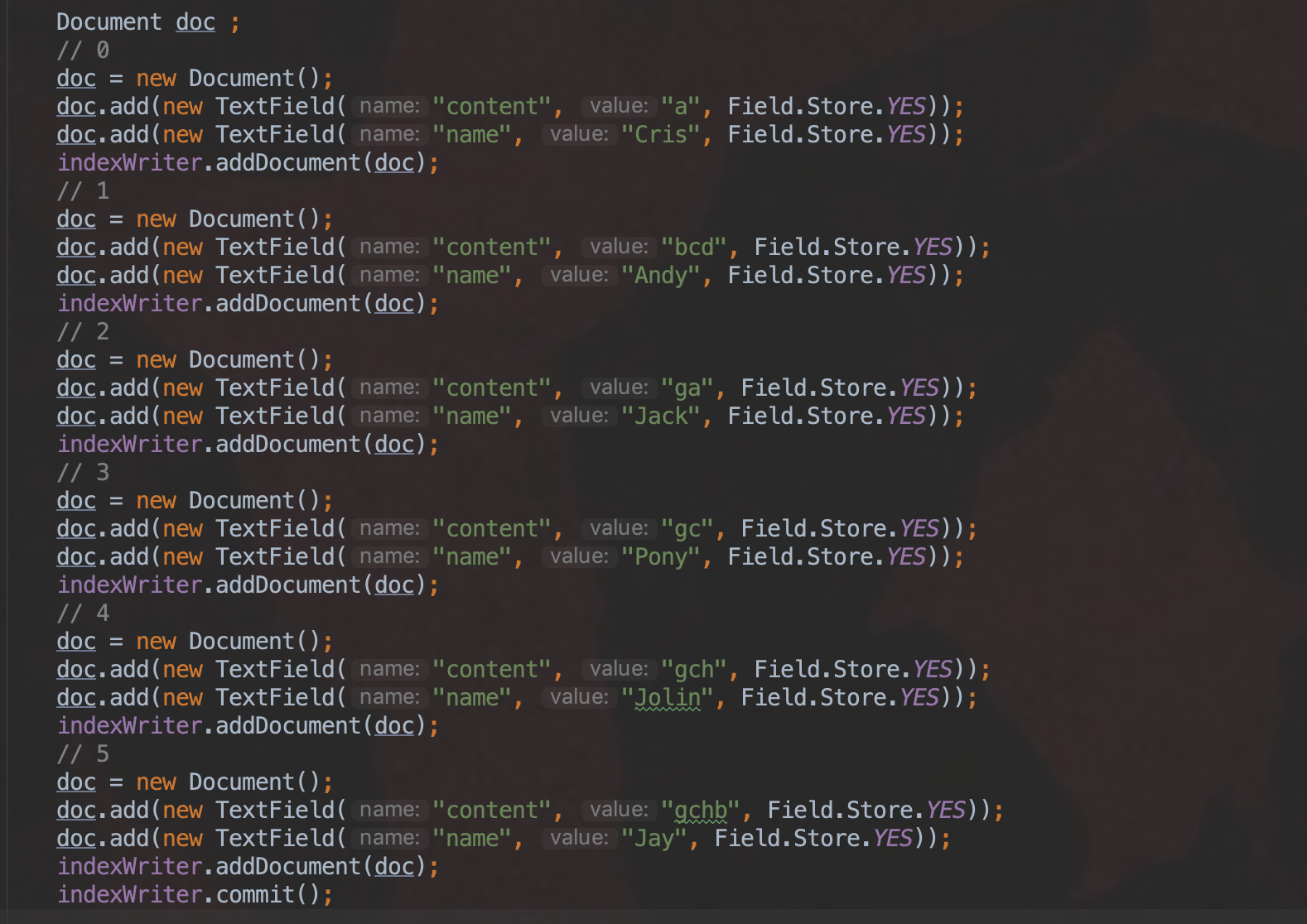：   查询条件： 图3：   生成DFA的过程本篇文章不会详细介绍，理由是如果能弄明白上面提到的DFA的概念，然后再去根据我注释的源码，相信很快能明白其逻辑过程。生成DFA全部过程的源码都在Automata.java文件中的Automaton makeBinaryInterval(...)方法中。GitHub地址：https://github.com/luxugang/Lucene-7.5.0/blob/master/solr-7.5.0/lucene/core/src/java/org/apache/lucene/util/automaton/Automata.java

转移图：

图4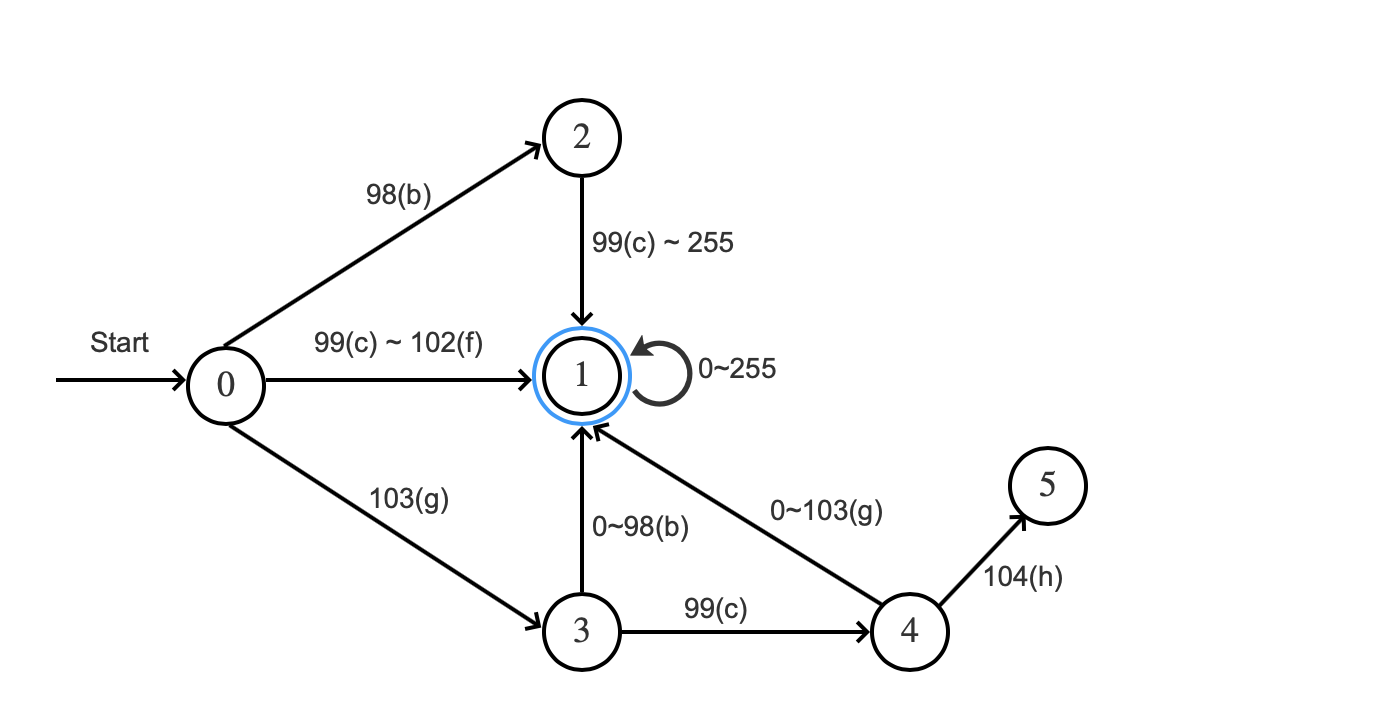：   上图中 数字为ASCII。   接受语言L(域值大于等于"bc"并且小于等于"gch")的自动机A的完整描述是 A = ({0，1，2，3，4，5}， {0，… ，255}， $\delta$$\delta$，0，{1，3，4，5})

筛选满足查询范围要求的域值

  由于我们在TermRangeQuery中指定的域名为“content”，所以Lucene会按照从小到大的顺序遍历所有域名为"content"的域值，即"a"、"bcd"、"ga"、“gc”、"gch"、"gchb"，然后对这些域值逐个的去DFA中查找，比如说"bcd"，总是从状态0开始，检查每一个字符"b"、"c"、"d"能否在DFA中通过转移分别找到各自的状态，或者找到一个可接受的状态（蓝色圆圈的状态），如果前面两个条件之一满足，那么我们认为"bcd"是满足在范围"bc"~"gch"中的。

转移函数

状态0的转移函数

  状态0有到状态1、状态2、状态3 一共三种转移方式，转移函数为：

状态1的转移函数

  状态1是一个可接受状态，转移函数为：

状态2的转移函数

  状态2有到状态1的一种转移方式，转移函数为：

状态3的转移函数

  状态3有到状态1、状态4的两种转移方式，转移函数为：

状态4的转移函数

  状态4有到状态1、状态5的两种转移方式，转移函数为：

状态5的转移函数

  状态5是一个终结状态，故没有转移函数。

处理 "a"

  “a”的ASCII码为97，无法通过转移函数完成转移，所以"a"不在查询范围内。

处理 "bcd"

图5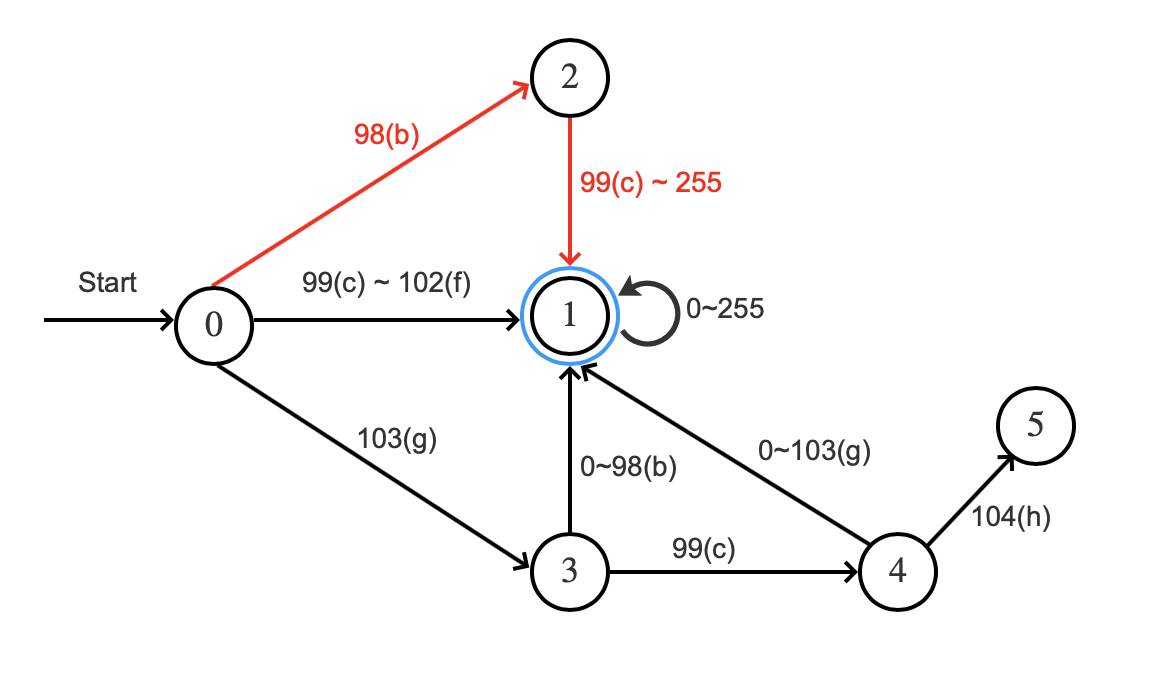：   “b”根据状态0的转移函数转移到状态2，"c"根据状态2的转移函数转移到状态1，此时已经到达可接受状态，所以无论后面是任意的一个或多个字符，都是满足查询范围要求的，例如"bcd"、"bcddf"、"bcasdfasdfasdfasdf"。

处理 "ga"

图6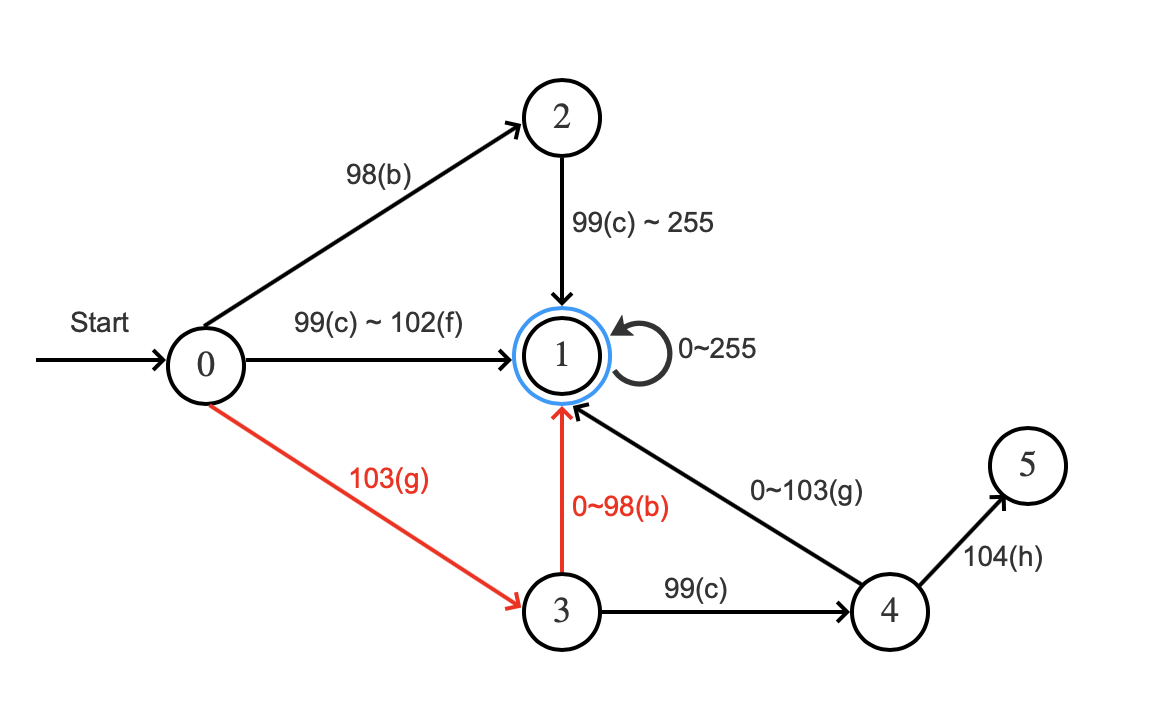：   "g"根据状态0的转移函数转移到状态3，"a"根据状态3的转移函数转移到状态1，此时已经到达可接受状态，所以无论后面是任意的一个或多个字符，都是满足查询范围要求的。

处理 "gc"

图7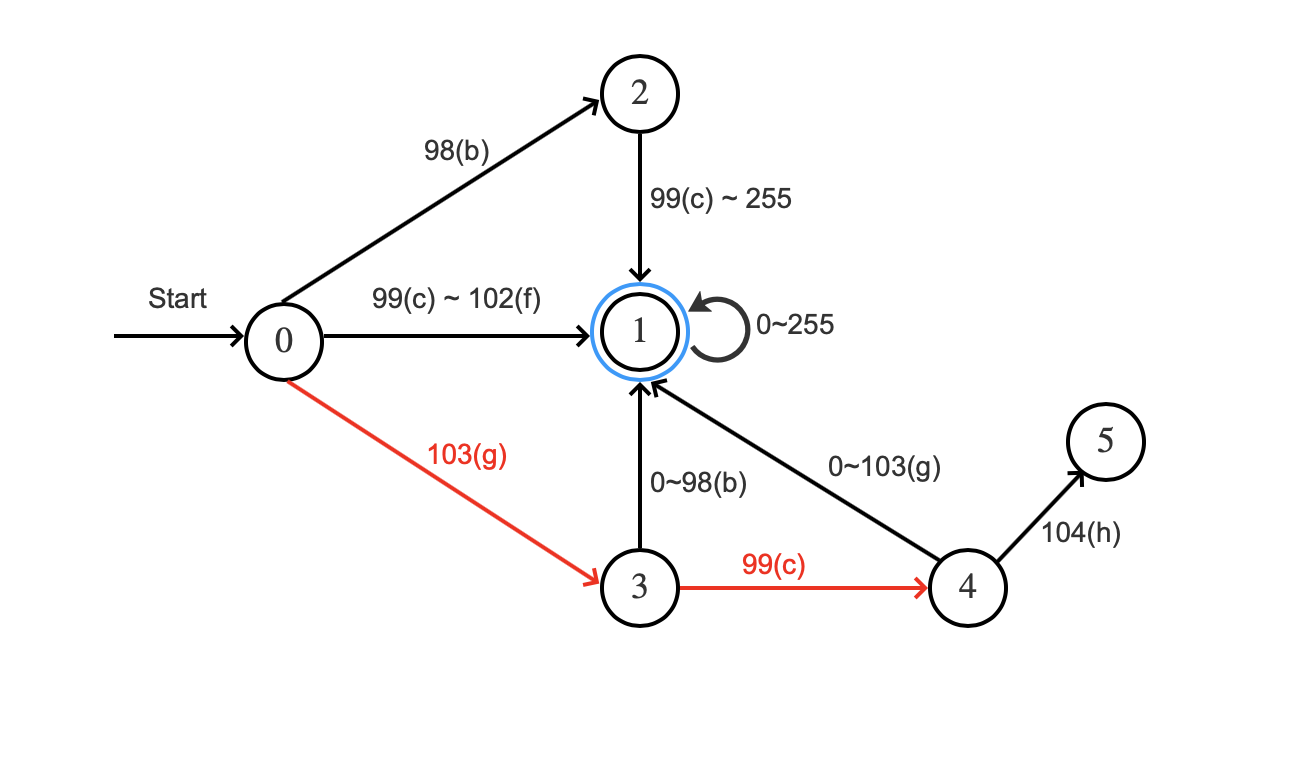：   "g"根据状态0的转移函数转移到状态3，"c"根据状态3的转移函数转移到状态4，由于后面没有字符，所以可以根据状态4的转移函数转移到状态0。

处理 "gch"

图8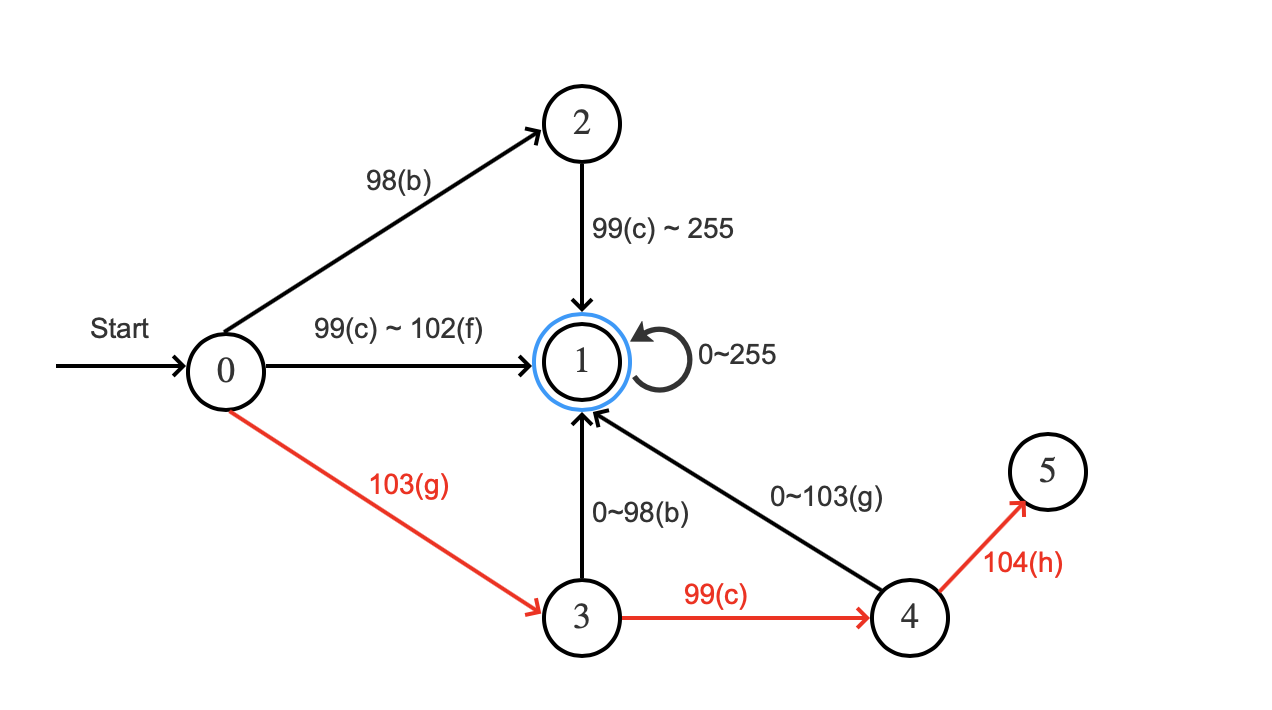：   "g"根据状态0的转移函数转移到状态3，"c"根据状态3的转移函数转移到状态4，"h"根据状态4的转移函数转移到状态5，状态5是一个终结状态，所以满足查询范围要求。

处理 "gchb"

  "g"根据状态0的转移函数转移到状态3，"c"根据状态3的转移函数转移到状态4，"h"根据状态4的转移函数转移到状态5，由于状态5是一个终结状态，所以无论出现哪个字符，都找不到下一个状态，所以不满足查询范围要求。

结语

  本文介绍了DFA在Lucene中的应用，是为介绍TermRangeQuery做一个前置知识，文中介绍DFA的内容纯粹是复制粘贴书籍<<自动机理论、语言和计算导论(原书第3版)>>中第二章第二小节的内容。