
介绍下一篇基于FMA(Fused Multiply-Add)利用SIMD的文章。
原文地址:https://www.elastic.co/search-labs/blog/articles/vector-similarity-computations-fma-style
原文
In Lucene 9.7.0 we added support that leverages SIMD instructions to perform data-parallelization of vector similarity computations. Now we’re pushing this even further with the use of Fused Multiply-Add (FMA).
What is FMA
Multiply and add is a common operation that computes the product of two numbers and adds that product with a third number. These types of operations are performed over and over during vector similarity computations.
图1:
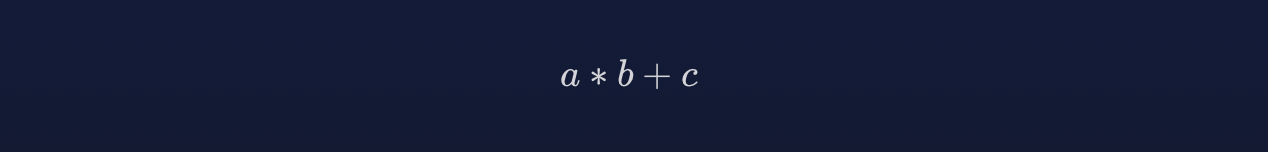
Fused multiply-add (FMA) is a single operation that performs both the multiply and add operations in one - the multiplication and addition are said to be “fused” together. FMA is typically faster than a separate multiplication and addition because most CPUs model it as a single instruction.
FMA also produces more accurate results. Separate multiply and add operations on floating-point numbers have two rounds; one for the multiplication, and one for the addition, since they are separate instructions that need to produce separate results. That is effectively,
图2:

Whereas FMA has a single rounding, which applies only to the combined result of the multiplication and addition. That is effectively,
图3:

Within the FMA instruction the a * b produces an infinite precision intermediate result that is added with c, before the final result is rounded. This eliminates a single round, when compared to separate multiply and add operations, which results in more accuracy.
Under the hood
So what has actually changed? In Lucene we have replaced the separate multiply and add operations with a single FMA operation. The scalar variants now use Math::fma, while the Panama vectorized variants use FloatVector::fma.
If we look at the disassembly we can see the effect that this change has had. Previously we saw this kind of code pattern for the Panama vectorized implementation of dot product.
1 | vmovdqu32 zmm0,ZMMWORD PTR [rcx+r10 |
The vmovdqu32 instruction loads 512 bits of packed doubleword values from a memory location into the zmm0 register. The vmulps instruction then multiplies the values in zmm0 with the corresponding packed values from a memory location, and stores the result in zmm0. Finally, the vaddps instruction adds the 16 packed single precision floating-point values in zmm0 with the corresponding values in zmm4, and stores the result in zmm4.
With the change to use FloatVector::fma, we see the following pattern:
1 | vmovdqu32 zmm0,ZMMWORD PTR [rdx+r11 |
Again, the first instruction is similar to the previous example, where it loads 512 bits of packed doubleword values from a memory location into the zmm0 register. The vfmadd231ps (this is the FMA instruction), multiplies the values in zmm0 with the corresponding packed values from a memory location, adds that intermediate result to the values in zmm4, performs rounding and stores the resulting 16 packed single precision floating-point values in zmm4.
The vfmadd231ps instruction is doing quite a lot! It’s a clear signal of intent to the CPU about the nature of the computations that the code is running. Given this, the CPU can make smarter decisions about how this is done, which typically results in improved performance (and accuracy as previously described).
Is it fast
In general, the use of FMA typically results in improved performance. But as always you need to benchmark! Thankfully, Lucene deals with quite a bit of complexity when determining whether to use FMA or not, so you don’t have to. Things like, whether the CPU even has support for FMA, if FMA is enabled in the Java Virtual Machine, and only enabling FMA on architectures that have proven to be faster than separate multiply and add operations. As you can probably tell, this heuristic is not perfect, but goes a long way to making the out-of-the-box experience good. While accuracy is improved with FMA, we see no negative effect on pre-existing similarity computations when FMA is not enabled.
Along with the use of FMA, the suite of vector similarity functions got some (more) love. All of dot product, square, and cosine distance, both the scalar and Panama vectorized variants have been updated. Optimizations have been applied based on the inspection of disassembly and empirical experiments, which have brought improvements that help fill the pipeline keeping the CPU busy; mostly through more consistent and targeted loop unrolling, as well as removal of data dependencies within loops.
It’s not straightforward to put concrete performance improvement numbers on this change, since the effect spans multiple similarity functions and variants, but we see positive throughput improvements, from single digit percentages in floating-point dot product, to higher double digit percentage improvements in cosine. The byte based similarity functions also show similar throughput improvements.
Wrapping Up
In Lucene 9.7.0, we added the ability to enable an alternative faster implementation of the low-level primitive operations used by Vector Search through SIMD instructions. In the upcoming Lucene 9.9.0 we built upon this to leverage faster FMA instructions, as well as to apply optimization techniques more consistently across all the similarity functions. Previous versions of Elasticsearch are already benefiting from SIMD, and the upcoming Elasticsearch 8.12.0 will have the FMA improvements.
Finally, I’d like to call out Lucene PMC member Robert Muir for continuing to make improvements in this area, and for the enjoyable and productive collaboration.
译文
在Lucene 9.7.0中,我们新增了支持,利用SIMD指令来执行数据并行化的向量相似度计算(vector Similarity)。现在,我们更进一步地使用了融合乘法加法(Fused Multiply-Add,FMA)。
What is FMA
乘法跟加法是一种常见的操作,它计算两个数字的乘积,并将该乘积与第三个数字相加。在向量相似度计算过程中,这些类型的操作会一次又一次地执行。
图1:
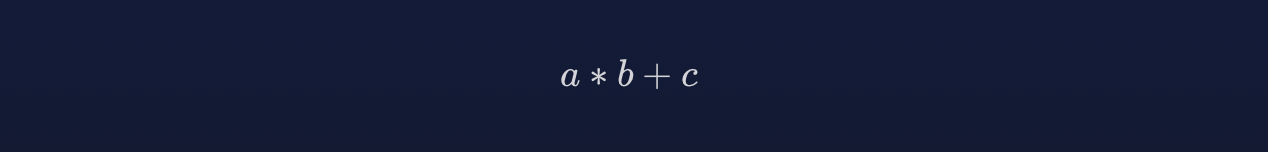
FMA是种单一操作,它在一次操作中执行了乘法和加法 - 乘法和加法被“融合”在一起。FMA通常比分开的乘法和加法更快,因为大多数CPU将其建模为单一指令。
FMA还能产生更准确的结果。分开的浮点数乘法和加法操作需要两轮,一轮用于乘法,一轮用于加法,因为它们是分开的指令,需要产生不同的结果。而FMA只有一轮舍入(round),这仅适用于乘法和加法的合并结果。这消除了与分开的乘法和加法操作相比的单一舍入,从而提高了准确性。
图2:

然而,FMA只进行一次舍入,而这个舍入只适用于乘法和加法的合并结果。相当于:
图3:

在FMA指令中,a * b会产生一个无限精度的中间结果,然后与c相加,最后对最终结果进行舍入。与分开的乘法和加法操作相比,这消除了一次舍入,从而提高了准确性。
Under the hood
那么发生了什么真正的改变呢?我们用单个FMA操作替换了分开的乘法和加法操作。scalar variants现在使用Math::fma,而Panama vectorized variants则使用FloatVector::fma。
如果观察下反汇编的结果,我们可以看到其发生的变化。之前对于这类代码模式,Panama对于点积的实现如下:
1 | vmovdqu32 zmm0,ZMMWORD PTR [rcx+r10 |
vmovdqu32 指令从内存位置加载512位 packed doubleword到zmm0寄存器中。接着,vmulps 指令将zmm0的值与来自内存位置的相应packed value相乘,并将结果存储在zmm0中。最后,vaddps 指令将zmm0中的16个packed 单精度的浮点值与zmm4中的相应值相加,并将结果存储在zmm4中。
使用FloatVector::fma后的变化,我们可以看下下面的模式:
1 | vmovdqu32 zmm0,ZMMWORD PTR [rdx+r11 |
再次的,第一条指令与之前的示例相似,它从内存位置加载512位packed doubleword values到zmm0寄存器中。然后,vfmadd231ps(这是FMA指令)将zmm0中的值与来自内存位置的相应packed values相乘,将中间结果添加到zmm4中,执行舍入,并将结果存储在zmm4中的16位packed single precision floating-point values。
vfmadd231ps指令执行了多个操作,明确告诉CPU代码正在运行的计算性质。基于这一信息,CPU可以更明智地决定如何执行操作,通常会导致性能改进(如前面所述)和更高的准确性。
Is it fast
总的来说,使用FMA通常会导致性能提升,但仍需要进行基准测试。不过Lucene在确定是否使用FMA时处理了许多复杂性(有些情况下不允许使用FMA,后续介绍向量搜索时会提到),因此用户不需要担心这些细节。这包括CPU是否支持FMA,Java虚拟机是否启用FMA,以及仅在已证明比分开的乘法和加法操作更快的架构上启用FMA。尽管可以看出这种启发式方法并不完美,但它在提供良好的开箱即用体验方面已经做了很多。使用FMA可以提高准确性,而未启用FMA时,现有的相似性计算没有负面影响。
除了使用FMA,向量相似性函数相关的内容(the suite of similarity functions)也进行了改进。 dot product、square 和 cosine distance 和Panama向量化都已更新。通过查看反汇编和实验经验应用了(apply)一些优化措施,这些措施带来了改进,有助于保持CPU忙碌的状态,主要通过更加的一致性和有针对性的循环展开(loop unrolling),以及消除循环内的数据依赖性。
-
mostly through more consistent and targeted loop unrolling:这是一种优化技术,通过增加循环体中代码的实例数量来减少循环的迭代次数。这种方法可以提高程序的执行效率,因为它减少了循环控制逻辑的开销,并可能使得更多的数据在单个循环迭代中被处理。
-
在循环内移除数据依赖(removal of data dependencies within loops):这是指修改循环中的代码,以减少或消除数据依赖,从而提高性能。数据依赖可能会导致循环迭代之间的延迟,因为后续的迭代可能需要等待前一个迭代完成数据处理。通过重构代码来减少这种依赖,可以使循环的不同迭代更加独立,从而提高运行效率。综合来看,这些技术有助于提高程序处理循环时的性能,特别是在涉及大量数据和复杂计算时。
具体的性能提升没那么直接通过数据来确定,因为影响涵盖了multiple similarity functions and variants,但我们看到了吞吐量方面的提升,从浮点型数值的点积操作的个位数百分比的提升到cosine操作的两位数百分比的提高。基于字节的相似性函数也显示出类似的吞吐量的提升。
Wrapping Up
在Lucene 9.7.0中,我们添加了通过SIMD指令来启用low-level primitive操作用于向量搜索。在即将发布的Lucene 9.9.0中,我们进一步利用更快的FMA指令,并更一致地应用于所有相似性函数的优化技术。早期版本的Elasticsearch已经受益于SIMD,即将发布的Elasticsearch 8.12.0将获得FMA改进。最后,我要感谢Lucene PMC成员Robert Muir在这个领域持续改进,并为愉快而富有成效的合作表示赞扬。
