NumericUtils（Lucene 9.8.0） | Lu Xugang的小屋

Lucene中用BKD存储的数值无论是哪种类型（long，int，float，double，BigInteger），为了便于使用相同的代码逻辑中实现BKD的遍历以及优化存储，都统一使用字节数组byte[]描述原值（original value）并且其转化成字节数组的逻辑都在NumericUtils类中实现。

long类型

我们看下long类型的值如何转化为字节数组。

因为long类型占用64bit，即8个字节（一个字节占8位），所以需要大小为8的字节数组。需要两步完成字节数组的转化：

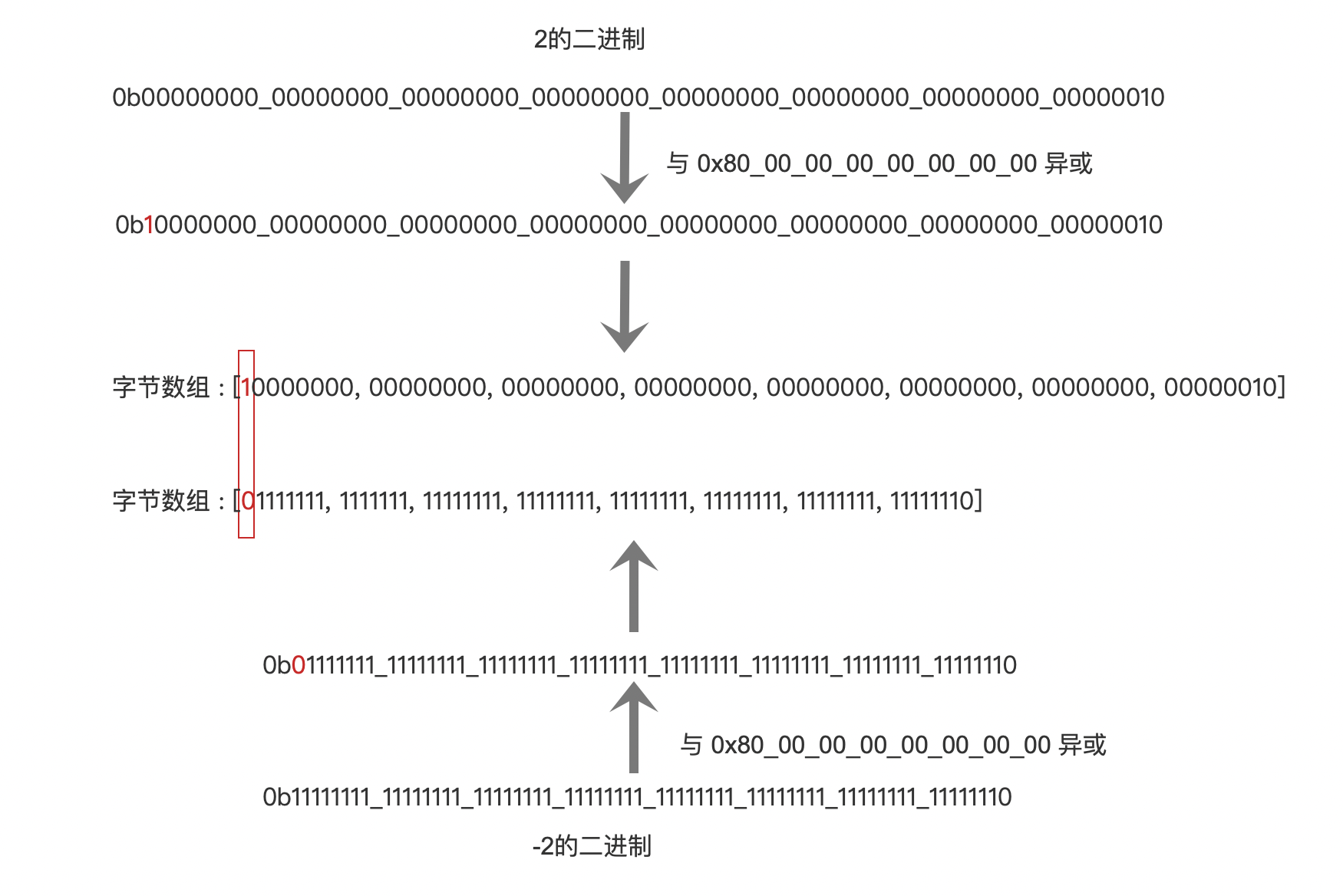
步骤一：将long中的最高位，即符号位，跟1执行异或操作。
- 为了在转化为字节数组后，能让字节数组依旧有拥有大小比较的能力
- 对于用字节数组表示的数值，是通过对字节数组中的每个元素进行二进制比较来判断大小。
  - 二进制的比较方式为：从最高位开始，逐位比较，当遇到第一个不相同的bit，那么bit为1的值大于bit为0的值
  - 不过在LUCENE-10145之后，不再是简单的两个字节数组的比较，这里简单提一下，使用更高效但依然是无符号的比较方式。
- 因此在long类型中，对于一个正数，它的最高位总是0，而负数的最高位是1，如果直接将符号位写入到字节数组，会出现所有的负数都大于正数的情况
步骤二：从long的最高位开始，每8个bit作为字节数组的一个数组元素。

例子

有两个long类型数值2跟-2其转化过程如下：

图1：

int类型

跟longToSortableBytes的处理逻辑是一致，差别就是生成的字节数组大小是4，而long类型转化成的字节数组大小为8。

double/float类型

Lucene中将double和float类型分别通过JDK提供的Double.doubleToLongBits(double value)以及Float.floatToIntBits(float value)将浮点型的数值转换成使用IEEE 754标准的值，即long跟int值，然后通过上文中的方法再进一步转化为字节数组。

IEEE 754

我们首先重新回顾下IEEE 754这个关于浮点数算术的国际标准。

double类型

对于双精度（64bit）的浮点数可以分为三个部分：

符号位：（1位），决定数值的正负。0 表示正数，1 表示负数。
指数位：（11位），用于表示数值的范围。这个部分决定了浮点数的大小。
- 指数位是结合偏移值（指数偏置，偏置值：1023）后的值，其中一个好处是可以将负指数跟正指数统一成正指数，那么在比较两个浮点的指数位时，比较两个无符号整数一样简单，不需要考虑正负。
尾数位：（52位）：也称为有效数位或小数位，用于表示数值的精度。

float类型

对于单精度（32bit）的浮点数可以分为三个部分：

符号位：（1位）：决定数值的正负。0 表示正数，1 表示负数。
指数位：（8位）：用于表示数值的范围。这个部分决定了浮点数的大小。偏置值：127
尾数位：（23位）：也称为有效数位或小数位，用于表示数值的精度。

转化

接着我们给出一个双精度转化的例子。比如我们有一个双精度的浮点数，也就是double类型的值：1024.0256。

步骤1：十进制转二进制

对浮点数的整数跟小数的十进制分别使用对应的规则转化为二进制：

1.1 整数

1024的二进制就是2^10。

1.2 小数

小数部分的计算逻辑如下：

0.0256 × 2 = 0.0512 → 取 0
0.0512 × 2 = 0.1024 → 取 0
0.1024 × 2 = 0.2048 → 取 0
0.2048 × 2 = 0.4096 → 取 0
0.4096 × 2 = 0.8192 → 取 0
0.8192 × 2 = 1.6384 → 取 1（取小数部分作为下一步骤的输入）
0.6384 × 2 = 1.2768 → 取 1
0.2768 × 2 = 0.5536 → 取 0
0.5536 × 2 = 1.1072 → 取 1
...

直到某一步的计算结果为0，或者超过尾数位的长度（双精度为52位）。最终小数部分的二进制是：000001101000110110111000101110101100011100 。

1.3 整合整数跟小数两部分

那么十进制1024.0256对应的二进制就是：10000000000.000001101000110110111000101110101100011100。

步骤2：规格化

将步骤1中的二进制格式化为1.xxxxx的形式并且计算出指数。

2.1 格式化

即1.0000000000000001101000110110111000101110101100011100 × 2^10，也就是对步骤1中的二进制的小数点往左移动10位。

2.2 指数偏移

执行2.1后计算出的指数为10，那么结合双精度的偏置值（1023），最终的指数值为：10 + 1023 = 1033，即10000001001。

步骤3：获取尾数部分

双精度格式中，尾数部分需要 52 位。从规格化的数中取出尾数部分（不包括开头的 1），如果不够 52 位，则用 0 补足。即0000000000000001101000110110111000101110101100011100。

步骤4：合成IEEE 754格式

对于这个双精度的浮点数：1024.0256，转化后的IEEE 754为：

符号位: 0 （1位）
指数位: 10000001001（11位）
尾数位: 0000000000000001101000110110111000101110101100011100（52位）

单精度的转化方式类似于双精度，这里不赘述。

负数的问题

尽管通过IEEE 754标准，我们可以将双精度/单精度的浮点数用long/int类型表示，但如果浮点数是负值，会存在以下的问题，我们以双精度为例：两个负的双精度浮点数在转化为long值后，这两个long值的大小关系会发生倒置，即不是转化前浮点数对应的大小关系。

例如我们有以下两个浮点数：-1.234和 -2.345，转成long类型后的值如下所示：

图2：

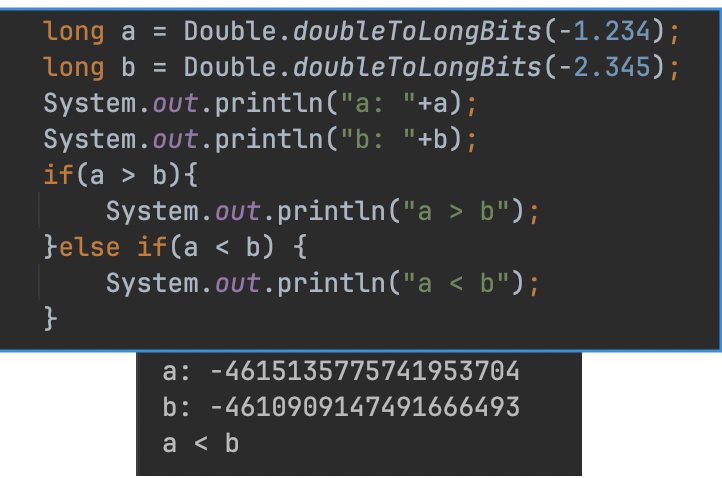
图2可知，long类型的a于b之间的大小关系跟转化前的浮点数之间的大小关系是相反的。而两个正数之间则不会发生这样的倒置：

图3：

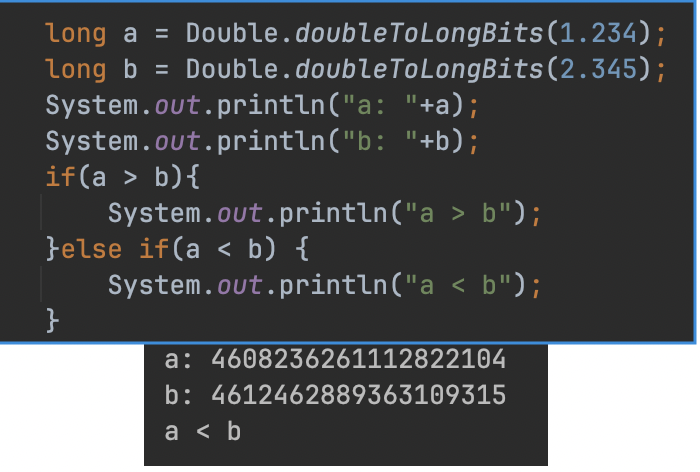
当然正/负的浮点数之间依然可以靠符号位保持原来的大小关系。所以要想一个办法，不能变更负数之间的大小关系。

异或操作

看下Lucene中是如何处理负数问题的：

图4：

图4中，bits为IEEE754标准的值。可以看到上述过程分为三步：

第一步：带符号的右移63位的目的是取出符号位
- 如果是正的浮点数，则结果为0，即所有bit位都是0
- 如果是负的浮点数，则结果为-1，即所有bit位都是1
第二步：与0x7fffffffffffffffL，这里需要注意的是 &的优先级比^高。
- 如果是正的浮点数，则结果为0b00000000_00000000_00000000_00000000_00000000_00000000_00000000_00000000
- 如果是负的浮点数，则结果为0b01111111_11111111_11111111_11111111_11111111_11111111_11111111_11111111
第三步：与IEEE754标准的值做异或操作
- 如果是正的浮点数，那么bits会与0b00000000_00000000_00000000_00000000_00000000_00000000_00000000_00000000异或，由于跟0执行异或操作时不会改变任何bit位，即不对bits做调整，所以正如图4的注释说到：or back to the original，也就是说这个方法不会变更正的浮点数
- 如果是负的浮点数，那么bits会与0b01111111_11111111_11111111_11111111_11111111_11111111_11111111_11111111异或，由于它的最高位是0，其他位都是1，也就是bits的符号位不变，并且其他位（指数位跟尾数位）都会取反。这样就能逆转两个负数之间的大小关系，解决了上述的负数问题
  - 为什么取反后就能逆转两个负数之间的大小关系：因为指数位跟尾数位是不考虑符号位的二进制比较